Mandelbrot set for computational competency

Mandelbrot set

The following codes were scripts written entirely by myself. References and information in regards to a Mandelbrot set were from its Wikipedia documentation. For scratch work to see my thought process you can click here to see my brainstorming off of the wiki page. The script is not the most computationally efficient but this is a demonstration of my capability to translate mathematical languages into scripts and to interpret of boundary conditions.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")

# Declaring the parameters for the sizes and resolutions
xmin =       -2 
ymin =       -1   
xmax =        1 
ymax =     xmax
resolution = 250
detail     = 250
xvec = np.linspace(xmin,xmax,resolution);
yvec = np.linspace(ymin,ymax,resolution);
re, im     = np.meshgrid(xvec, yvec);
c          = re + im*1j;
row    = len(re);
column = len(im);
EscVal = np.zeros(shape=(row,column)); # zero matrix generated to allow storage of escape values
LastVal= np.zeros(shape=(row,column)); # zero matrix generated to allow storage of last value of zn

for a in range(1,row):
    for b in range(1,column):
        cval = c[a,b]
        zn       = 0;
        iteration= 0;
        detail   = detail;
        while iteration < (detail + 1):
            zn = (zn)**2 + cval
            Norm = abs(zn)
            EscVal[a,b] = Norm
            iteration = iteration + 1
            if  Norm > 2 :
                break
            LastVal[a,b]=zn

plt.pcolormesh(re,im,EscVal)
plt.xlabel('Real axis'), plt.ylabel('imaginary axis');
plt.title('Complex space plot of Mandelbrot set');
plt.grid(color = 'grey', linestyle='-',linewidth = 0.5)

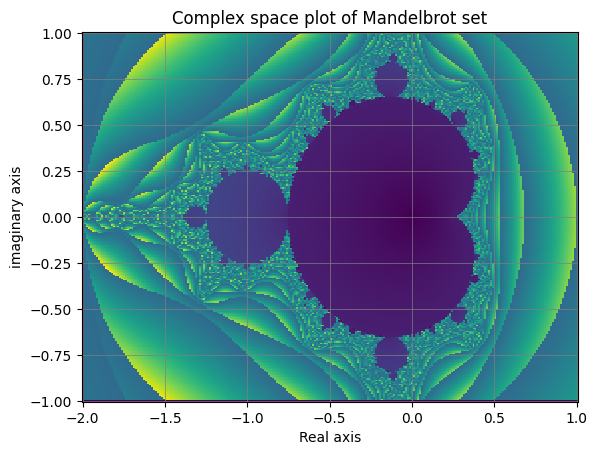
Justifications:

Question: What is a mandelbrot set?

By wikipedia definition, the mandelbrot set is a set of numbers that iterates through the recursion relation, such that you yield different characteristics of the set of numbers.

Definition 1

A Mandelbrot set is characterized by the recursion relation of

(1)\[z_{n+1}=z_n^2+c\]

where \(c\) is any complex number within the interval of the real domain \(x\in[-2,1]\) and of the imaginary domain \(y\in[-1,1]\), given that \(c=x+iy\) .

A condition is imposed for the complex number to be in the Mandelbrot Set:

(2)\[|z|\leq2\]

If the complex number \(c\) iterates through the recursion relation in equation (1) and satisfies the condition in equation (2), then \(c\) is within the mandelbrot set.

If the complex number \(c\) iterates through the recursion relation in equation (1) and does not satisfy the condition in equation (2), then \(c\) is not in the mandelbrot set. Note that the numbers that are not in the Mandelbrot set can diverge to infinity.

For other chaotic behavior and its connection to the bifurcation diagram, refer to wikipedia.